이전 글에서 회귀 문제의 경우 평가 지표를 알아보았다.
분류 문제에서는 어떤 평가 지표를 사용하는지 알아보자
Confusion Matrix

먼저 confusion matrix를 알 필요가 있다.
- 실제값이 True일 때, 예측값이 True이면 True Positive, TP
- 실제값이 False일 때, 예측값이 True이면 False Positive, FP
- 실제값이 True일 때, 예측값이 False이면 False Negative, FN
- 실제값이 Negative일 때, 예측값이 Negative이면 True Negative, TN
이렇게 정의한다.
True ~~ 일 때 정답을 맞춘 것이다.
참고로
FP(False Positive)의 경우 Type 1 Error라고 하며
FN(False Negative)의 경우 Type 2 Error라 한다.
Accuracy; 정확도
일반적으로 생각할 수 있는 평가지표로
전체 케이스 대비 정답을 맞춘 비율이다.
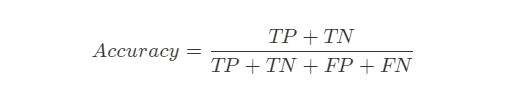
정확도는 보편적으로 사용되지만,
데이터의 편향이 심한 케이스에서는 좋은 평가지표로 활용될 수 없다.
데이터의 편향이란 데이터가 골고루 분포하지 않고 한 쪽으로 치우치게 많은 경우를 말한다.
대표적으로 CT 암을 판별하는 경우를 예시로 들 수 있다.
이 경우 음성 환자, 즉 암이 아닌 환자의 수가 절대적으로 많다.
100명 중 2명만 암 환자인 데이터가 있다고 치자.
이때 모델을 학습하지 않고 전체 예측을 음성으로 출력하기만 해도
정확도는 98%가 나올 것이다.
이런 경우에 사용할 수 있는 다른 평가 지표들이 있다.
Recall; 재현율
Sensitivity 또는 Hit rate, True positive Rate 라고도 한다.

실제 정답이 Positive인 것들 중에 정답을 맞춘 비율로 해석할 수 있다.
재현율을 이용해서 위의 예시 경우를 평가하면
재현율이 0%가 나온다.
양성 2개 중 하나도 맞추지 못했기 때문이다.
보통 재현율 하나로만 평가 지표를 확인하기는 힘들다.
또 다시 전체 예측을 양성으로 출력하게 한다면 재현율이 100%가 될 것이기 때문이다.
따라서 아래의 정밀도와 함께 비교해야할 필요가 있다.
Precision; 정밀도

Positive로 예측한 것들 중에 진짜 Positive의 비율로 해석할 수 있다.
정밀도가 높으면 오검출률이 낮음을 의미한다.
일반적으로 Recall과 Precision은 반비례의 관계를 가진다.
재현율을 높이려고 하면 오검출률이 높아지고(= 정밀도가 낮아지고)
오검출률을 낮추려하다 보면 검출량이 낮아지기(= 재현율이 낮아지기) 때문이다.
Fall out
False Negative rate라고도 한다.

실제 Positive값을 Negative로 예측한 비율을 의미한다.
-> 오검출률
F1 score
Precision과 Recall의 조화평균.

F1 score는 0~1사이의 값을 가지며 높을수록 좋다.
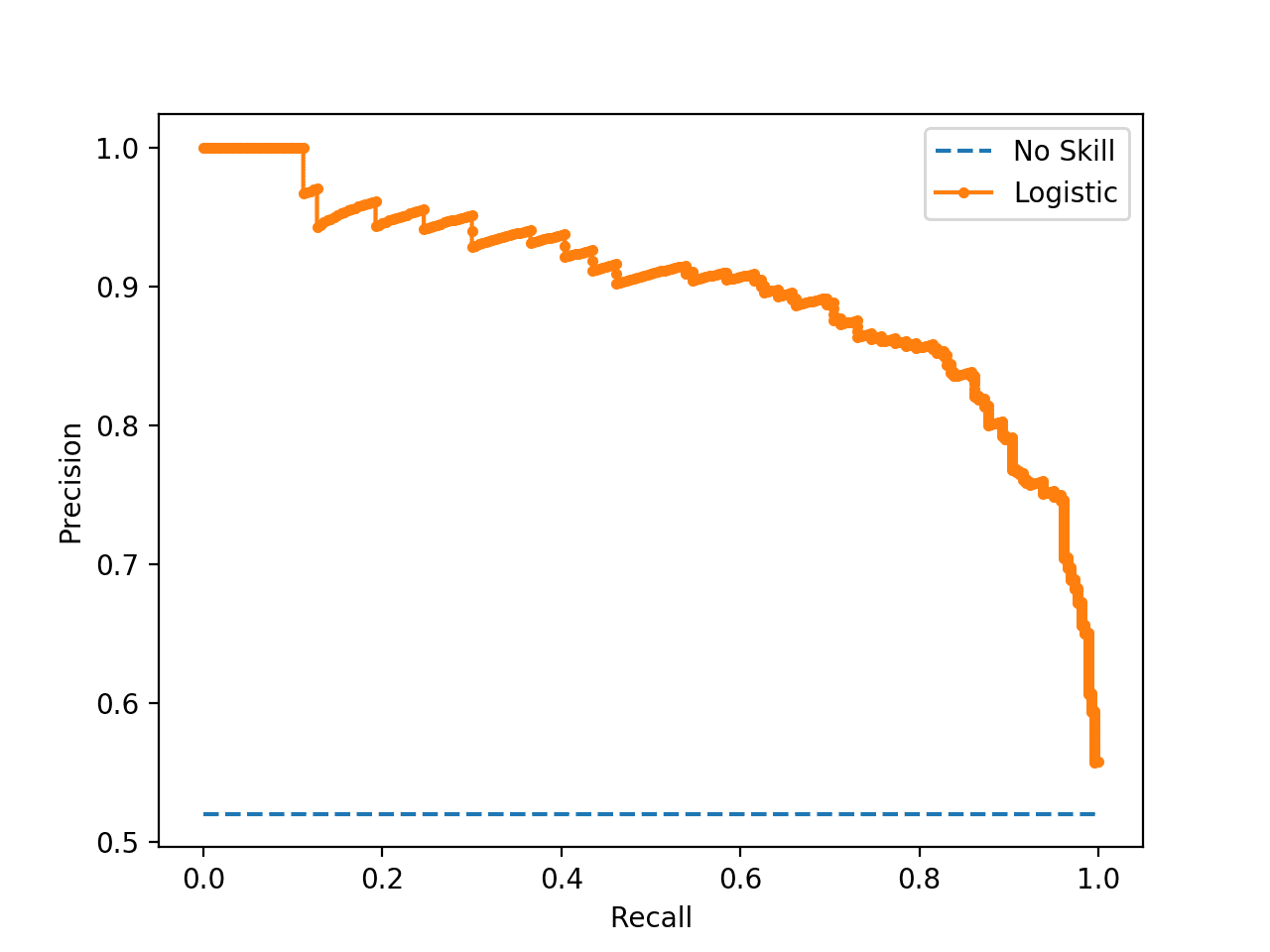
Precision - Recall graph
Precision과 Recall의 관계를 나타내는 그래프이다.
Precision을 y축, Recall을 x축에 나타낸다.
ROC curve
Recall과 Fall-out을 나타낸 그래프이다.
Fall-out(False Negative rate)이 x축, Recall(True positive Rate)이 y축에 나타낸다.

위의 두 그래프 모두 그래프가 위쪽에 있어야 좋은 모델이라고 할 수 있다.
Log - loss
위에서 알아본 평가지표는 주로 이항분류에서 사용하며
Log - loss는 주로 다항분류에서 사용하는 지표이다.

고양이, 개, 호랑이를 분류하는 모델을 만든다고 가정해보자
두 모델을 만들었는데 두 모델 모두 고양이 사진이 주어졌을때 고양이라고 예측한다.
하지만 A 모델은 고양이, 개, 호랑이일 확률을 차례로 0.8, 0.1, 0.1으로 예측했고,
B 모델은 0.5, 0.2, 0.3으로 예측했다고 하면
A와 B모델 중 어떤 모델이 더 나은 모델인가 생각해보면 A라고 대답할 수 있다.
이와 같은 경우에 모델을 측정하는 것이 Log loss 이다.
그림으로 살펴보는 다양한 성능 평가 방법들
비전 관련된 논문을 읽어보셨다면, Accuracy와 Precision 정도는 들어봤을겁니다. 어떠한 측정 시스템의 성능을 나타내는 지표에는 정말 다양한 방법이 있습니다. 위 표를 보고 있자니, 머리가 아득
eungbean.github.io
How to Use ROC Curves and Precision-Recall Curves for Classification in Python
It can be more flexible to predict probabilities of an observation belonging to each class in a classification problem rather […]
machinelearningmastery.com
'AI' 카테고리의 다른 글
| [CNN] Pooling (0) | 2022.04.14 |
|---|---|
| Computer vision에 들어가기 전 - Digital Image와 처리 (0) | 2022.04.13 |
| [ML] Model Evaluation & Regression Metrics (0) | 2022.04.08 |
| [ML] Linear Regression 구현, sklearn과 비교 (0) | 2022.03.29 |
| [ML] Linear Regression (0) | 2022.03.28 |
