[ML] Linear Regression

Heaea 2022. 3. 28. 21:46

Linear Regression

회귀란?

쉽게 말하면 어떤 데이터에 대해서 그 데이터에 영향을 주는 조건들의 영향력을 고려하여 데이터에 대한 조건부 평균을 구하는 기법이다.

회귀모델은 여러 조건 하에 평균을 추정할 수 있게하는 효율적인 방법이다.

Linear Regression 선형 회귀는 일차식을 이용한 회귀모델이다

독립 변수가 하나일 때는 단변량 선형회귀, 둘 이상일때는 다변량 선형회귀라고 한다.

y_i = wx_i +b

$w = weigt, b= bias$

다음과 같은 데이터가 있을 때 시험점수 몇 점을 받을까를 공부 시간이라는 변수 하나만 가지고 예측하는 것이 단변량 회귀분석이라고 할 수 있다.

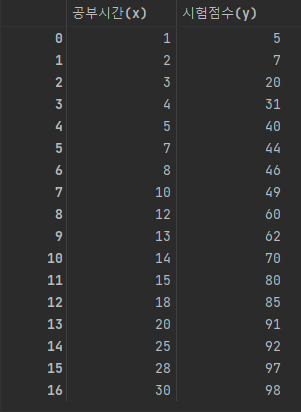
이 데이터를 scatter로 시각화하면 다음과 같다.

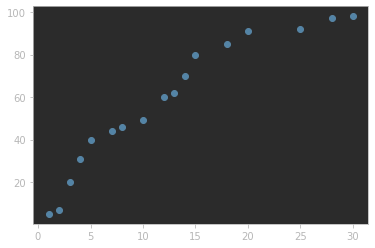
최초에는 weight과 bias를 random하게 설정한다.

임의로 wetight = 5, bias = -7 설정하면 선형회귀 식은 $y_i = 5x_i - 7$ 이 된다.

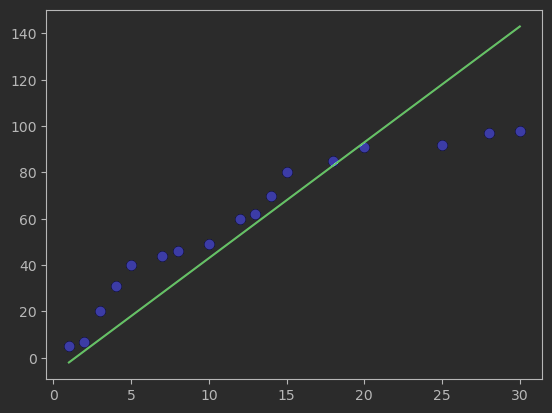
초록색 선으로 나타난 것이 예측 모델인데 데이터를 나타낸 파란색 점들과는 차이가 있다

예측값과 실제값의 차이를 오차, loss, error 등으로 표현하며

다음 그림에서 모두 표현하지는 않았지만 빨간선으로 나타낸 것들을 의미한다.

Loss = y_i - \hat y_i

$\hat y_i = wx_i + b$

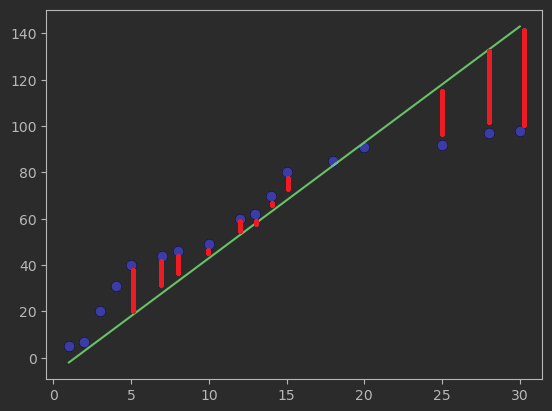
이제 해야 할 일은 loss값을 줄이는 것이다.

손실 값을 나타내는 함수 Loss fuction(또는 cost fuction)은 대표적으로 MSE가 있다.

MSE; mean square error; 최소제곱오차

MSE = {1 \over n}\sum^n_{i=1}(y_i - \hat y_i)^2

E(w,b) = {1 \over n}\sum^n_{i=1}(y_i - (wx_i+b))^2

loss fuction은 w와 b의 식으로 나타낼 수 있다.

위의 loss fuction을 최소로 만드는 w와 b를 찾는 과정이 머신러닝에서 learning의 과정이다.

그래프로 나타내면 이와 같은데

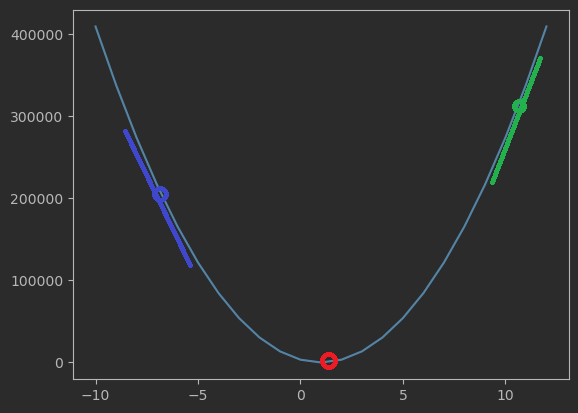
그래프에 나타난 함수가 최소인 지점. 즉 오차가 최소인 지점은 빨간색 부분이다.

저 지점의 w, b 값이 단변량 회귀분석의 최적 파라미터가 된다.

그렇다면 최초에 임의로 설정한 w, b값에서 최적의 값으로 찾아가야한다.

이때 사용하는 방법이 Gradient descent이다

함수의 기울기를 구하고 기울기의 절댓값이 최소가 되도록 조금씩 이동시킨다.

loss function을 미분하면 특정한 지점에서의 기울기를 찾을 수 있다.

위의 그래프에서 초록색이나 파란 지점의 접선의 기울기를 보면

초록색을 양의 기울기 파란색은 양의 기울기이나 그 절댓값이 크다는 것을 알 수 있다

이차식에서 값이 최소가 되는 지점은 접선의 기울기가 0인 지점이듯이

loss가 최소가 되는 지점은 접선 기울기의 절댓값이 최소인 지점이다.

(모든 함수에서 절대적인 것은 아니다!)

기존의 파라미터에서 미분값을 빼서 새로운 파라미터를 구하는 것을 반복하여 최적 파라미터로 다가간다.

w' = w - \lambda {\partial E(w,b) \over \partial w}

b' = b - \lambda {\partial E(w,b) \over \partial b}

$\lambda = learning$ $rate$

미분값을 그대로 사용하지 않고 앞에 $\lambda$ , learning rate를 곱해 사용하는데,

이는 파라미터 값이 급격하게 변하는 것을 방지하기 위함이다.

w, b값을 최적이 될 때까지 위와 같은 방식으로 업데이트 해나간다.

최적값을 찾으면 학습이 종료된다.

다변량 회귀분석은 독립 변수가 둘 이상인 것을 말한다.

실제로 시험 점수를 결정하는 요인은 공부 시간만으로 측정할 수 없다.

따라서 종속변수를 예측하는데 다수의 독립변수를 사용하는 경우가 많다.

다변량 선형회귀분석의 일반식은 다음과 같다.

\hat y = \beta_0 + \sum^n_{i=1}\beta_ix_i