다이나믹프로그래밍에 첫 번째 문제이다.
다이나믹 프로그래밍, 즉 동적계획법은
메모리를 더 사용하지만 실행 시간을 줄일 수 있는 기법이다
1. 큰 문제를 작은 문제로 나눌 수 있고
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일할 때
동적 계획법을 사용할 수 있다.
(참고 : https://techblog-history-younghunjo1.tistory.com/183)
재귀용법을 사용해서 피보나치 수를 구현하게 되면
작은 수에 대한 피보나치 함수를 반복해서 호출하게 된다.
fibonacci(3)을 호출하면 다음과 같은 일이 일어난다.
fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
두 번째 호출한 fibonacci(1)은 1을 출력하고 1을 리턴한다.
fibonacci(0)은 0을 출력하고, 0을 리턴한다.
fibonacci(2)는 fibonacci(1)과 fibonacci(0)의 결과를 얻고, 1을 리턴한다.
첫 번째 호출한 fibonacci(1)은 1을 출력하고, 1을 리턴한다.
fibonacci(3)은 fibonacci(2)와 fibonacci(1)의 결과를 얻고, 2를 리턴한다.
1은 2번 출력되고, 0은 1번 출력된다. N이 주어졌을 때,
fibonacci(N)을 호출했을 때, 0과 1이 각각 몇 번 출력되는지 구하는 프로그램을 작성하시오.백준 1003 문제에서 이를 찾아볼 수 있다.
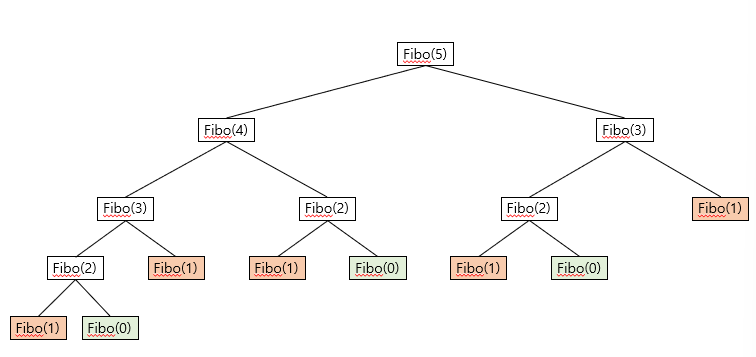
시각적으로도 표현해보았다.
반복실행에서 오는 시간 낭비를 줄이기위해
메모제이션 기법, 캐싱기법을 사용하는 것이 다이나믹 프로그래밍이다.
이미 실행한 함수에 대한 결과를 따로 저장해두고 그 값이 필요할 때 찾아서 쓰는 방식이다.
따라서 1003번 문제는 일반적인 재귀용법으로 풀면 시간초과가 나는 문제이다.
메모제이션 기법을 사용해서 구현한 피보나치 함수는 다음과 같다.
memo = [0 for i in range(41)]
memo[1] = 1
def fibo(n):
if n==0 :
return n
elif n==1 :
return n
else :
if memo[n] != 0 :
return memo[n]
memo[n] = fibo(n-1) + fibo(n-2)
return memo[n]재귀로만 구현한 코드와 비교했을 때,
def fibo(n):
if n==0 :
return n
elif n==1 :
return n
else :
return fibo(n-1) + fibo(n-2)memo라는 리스트에 함수 실행 결과를 저장하고, 이미 그 값이 있다면 함수를 실행하지 않고 값을 찾아서 이용한다.
문제
1003번 문제에서는
fibo(0), fibo(1)이 수행된 횟수를 출력해야 한다.

위의 그림에서 각각의 호출 횟수를 세어보았다.
fibo(3)이 호출되면 fibo(1)은 2번 fibo(0)은 1번 호출된다.
fibo(4)가 호출되면 fibo(1)과 fibo(0)은 각각 3번, 2번
fibo(5)의 경우 5번, 3번임을 알 수 있다
그림에서는 나타나지 않지만
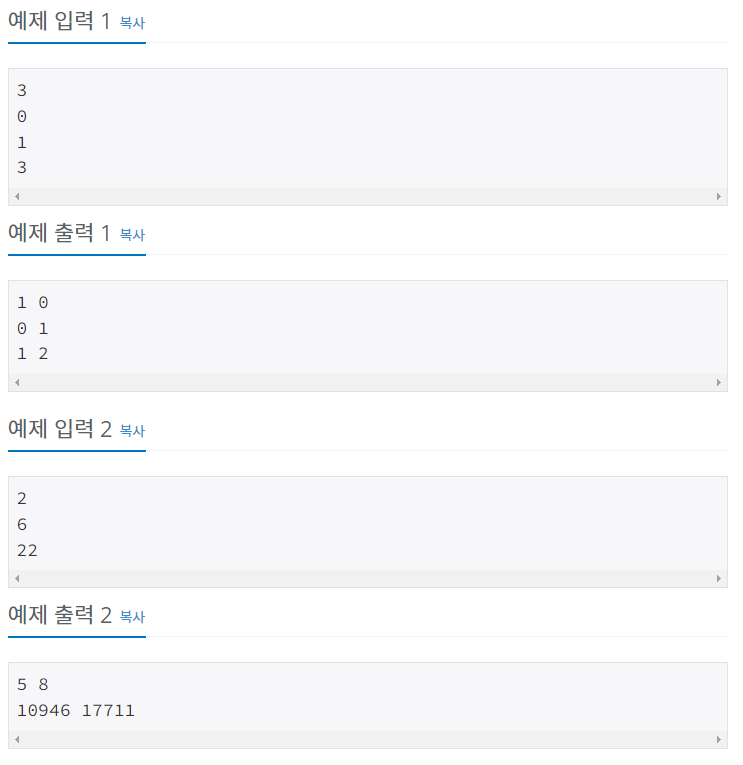
백준 예제로 알 수 있듯이
fibo(6)의 경우에는 8번, 5번씩 호출된다.
결과들을 찾다보니 규칙성이 발견되었다.


fibo(n)이 실행되면 fibo(1)은 n번째 피보나치 수만큼, fibo(0)은 n-1번째 피보나치 수 만큼 호출이 된다.
이 규칙을 따라 코드를 작성하면 다음과 같다.
memo = [0 for i in range(41)]
memo[1] = 1
def fibo(n):
if n==0 :
return n
elif n==1 :
return n
else :
if memo[n] != 0 :
return memo[n]
memo[n] = fibo(n-1) + fibo(n-2)
return memo[n]
import sys
input = sys.stdin.readline
x = int(input())
for i in range(x):
f = int(input())
if f == 0 :
print(1,0)
else :
if memo[f] == 0 :
fibo(f)
print(memo[f-1], memo[f])fibo(n)에 n이 0일 경우의 예외처리만 해주면
memo에서 값을 찾아서 결과값을 출력할 수 있다.
'Algorithm' 카테고리의 다른 글
| [백준][4779] python - 칸토어 집합 (0) | 2023.08.11 |
|---|---|
| [백준][7576][python] 토마토 - BFS (0) | 2023.08.09 |
| [정렬] 안정정렬(stable)과 불안정정렬(not stable) (0) | 2022.03.25 |
| [정렬] Quick Sort (0) | 2022.03.25 |
| [BOJ][python] 수 정렬하기 3 - 10989 (0) | 2022.03.21 |
