그래프는 연결되어 있는 객체 간의 관계를 표현하는 자료구조이다.
트리는 그래프의 일종으로 나무를 뒤집어 놓은 모양이며, 객체 간 상하 관계(부모-자식)가 있어 간선이 하위 노드 방향으로만 이어진다.
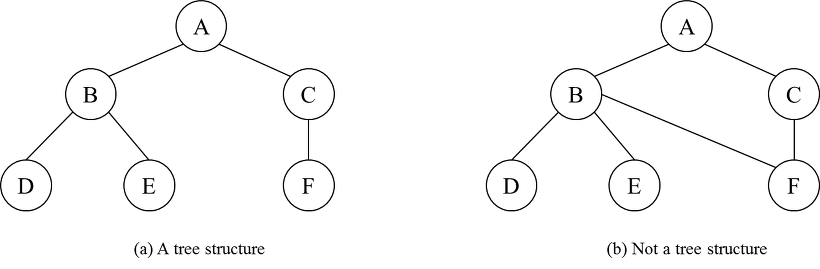
(a)는 트리이고 (b)는 그래프이다.
각 지점은 노드(node) 또는 정점(Vertices)라 부르고, 노드들을 있는 선은 간선(edge) 또는 링크(link)라고 한다.
그래프는 G(V,E)로 표시한다. V(G)는 그래프G의 정점들의 집합을 의미하며, E(G)는 간선들의 집합을 의미한다.
차수는 노드에 연결된 간선의 개수를 말한다.
- 그래프의 종류
무방향 그래프 : 노드들을 잇는 간선에 방향이 없는 그래프를 말한다. 무방향 그래프에서 차수(degree)는 노드에 연결된 다른 정점의 수이다. 간선들의 집합을 ()로 표시한다.

ex) E(G1)={(A,B), (A,D), (B,D), (B,C), (C,D)}
방향 그래프 : 간선에 방향이 있는 그래프이다. 방향그래프의 차수는 진입차수와 진출차수로 구분되어 나타난다. 간선들의 집합은 <>로 나타난다.

ex) G2={<A,B>, <A,D>, <B,D>, <B,C>, <D,C>}
가중치 그래프: 네트워크라고도 하며, 간선에 비용 또는 가중치가 할당되어있다.
그래프 G의 정점들의 집합의 부분집합과 간선들의 집합의 부분집합으로 이루어진 그래프를 그래프 G의 부분그래프라고 한다.
연결 그래프 : 그래프의 모든 정점에 대한 경로가 존재하는 그래프, 쉽게말해 그래프의 노드들이 간선으로 모두 연결되어 있는 그래프이다.
완전 그래프 : 모든 정점이 연결되어 있는 그래프
- 트리
그래프이며, 연결되어있고, 방향성이 없고, 순환이 없는 그래프.
트리에 조건에서 연결성을 빼면 포레스트이다.
- 그래프의 구현방법
1. 인접 리스트
2. 인접 행렬
-> 다음글에 계속!
- 그래프 탐색
넓이 우선 탐색 BFS(breath first search), 깊이 우선 탐색 DFS(depth first search)이 있다.

BFS : 시작 정점으로부터 가까운 정점부터 방문하는 순회방법이다. 큐를 사용한다. global한 답을 찾을 수 있지만 시간이 오래 걸리며 저장해야하는 양이 많다.
DFS : 시작정점에서 가장 깊이 갈 수 있을때까지 간 후 가장 가까운 갈림길로 돌아와서 다시 깊게 내려가는 순회방법이다. 스택이나 재귀를 사용한다. 찾은 답이 global이 아닐 수 있다.(최단 경로가 아닐 수 있다.)
'Algorithm' 카테고리의 다른 글
| [정렬] Quick Sort (0) | 2022.03.25 |
|---|---|
| [BOJ][python] 수 정렬하기 3 - 10989 (0) | 2022.03.21 |
| [재귀함수]하노이탑 (0) | 2021.12.12 |
| [Java][백준] 10828 스택 & String & BufferedReader (0) | 2021.10.23 |
| [python][programmers] 정렬 - k번째수 (0) | 2021.10.05 |
